Part Of A Musical Scale

The C major scale, ascending and descending
In music theory, a calibration is any set up of musical notes ordered past primal frequency or pitch. A scale ordered by increasing pitch is an ascending calibration, and a scale ordered by decreasing pitch is a descending calibration.
Ofttimes, especially in the context of the common practise period, virtually or all of the melody and harmony of a musical work is congenital using the notes of a single scale, which tin exist conveniently represented on a staff with a standard key signature.[ane]
Due to the principle of octave equivalence, scales are generally considered to bridge a single octave, with higher or lower octaves only repeating the pattern. A musical scale represents a sectionalisation of the octave space into a certain number of calibration steps, a scale step being the recognizable distance (or interval) between two successive notes of the scale.[two] However, there is no demand for scale steps to be equal within whatever scale and, especially equally demonstrated by microtonal music, there is no limit to how many notes can be injected within whatever given musical interval.
A measure of the width of each scale step provides a method to classify scales. For instance, in a chromatic scale each scale footstep represents a semitone interval, while a major scale is defined by the interval pattern W–W–H–W–Due west–W–H, where West stands for whole step (an interval spanning ii semitones, e.one thousand. from C to D), and H stands for one-half-step (e.m. from C to D ♭ ). Based on their interval patterns, scales are put into categories including diatonic, chromatic, major, minor, and others.
A specific scale is divers by its characteristic interval pattern and by a special note, known every bit its offset caste (or tonic). The tonic of a scale is the note selected as the beginning of the octave, and therefore as the beginning of the adopted interval blueprint. Typically, the name of the scale specifies both its tonic and its interval pattern. For example, C major indicates a major scale with a C tonic.
Groundwork [edit]
Scales, steps, and intervals [edit]
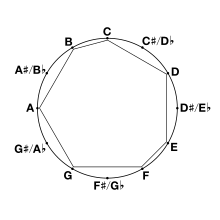
Scales are typically listed from low to high pitch. Most scales are octave-repeating, meaning their pattern of notes is the same in every octave (the Bohlen–Pierce scale is one exception). An octave-repeating scale can exist represented as a circular organization of pitch classes, ordered by increasing (or decreasing) pitch grade. For instance, the increasing C major scale is C–D–E–F–One thousand–A–B–[C], with the subclass indicating that the last note is an octave higher than the commencement note, and the decreasing C major scale is C–B–A–One thousand–F–E–D–[C], with the bracket indicating an octave lower than the first note in the calibration.
The distance between two successive notes in a calibration is called a scale step.
The notes of a scale are numbered by their steps from the first degree of the calibration. For example, in a C major scale the commencement annotation is C, the second D, the third E and then on. 2 notes tin also be numbered in relation to each other: C and Eastward create an interval of a third (in this instance a major 3rd); D and F as well create a third (in this example a minor third).
Pitch [edit]
A single scale tin be manifested at many different pitch levels. For case, a C major calibration can be started at C4 (centre C; run into scientific pitch notation) and ascending an octave to C5; or it could be started at C6, ascending an octave to C7.
Types of calibration [edit]
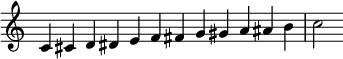
Scales may be described according to the number of unlike pitch classes they incorporate:
- Chromatic, or dodecatonic (12 notes per octave)
- Nonatonic (ix notes per octave): a chromatic variation of the heptatonic blues scale
- Octatonic (8 notes per octave): used in jazz and modern classical music
- Heptatonic (7 notes per octave): the well-nigh common modern Western calibration
- Hexatonic (6 notes per octave): common in Western folk music
- Pentatonic (5 notes per octave): the anhemitonic form (lacking semitones) is mutual in folk music, especially in Asian music; also known as the "black note" calibration
- Tetratonic (4 notes), tritonic (3 notes), and ditonic (2 notes): generally limited to prehistoric ("archaic") music
Scales may also be described by their elective intervals, such as being hemitonic, cohemitonic, or having imperfections.[3] Many music theorists concur that the constituent intervals of a scale have a large role in the cognitive perception of its sonority, or tonal character.
"The number of the notes that make upwardly a scale as well as the quality of the intervals betwixt successive notes of the scale help to give the music of a civilization area its peculiar sound quality."[four] "The pitch distances or intervals among the notes of a calibration tell us more about the audio of the music than does the mere number of tones."[5]
Scales may also be described by their symmetry, such as being palindromic, chiral, or having rotational symmetry every bit in Messiaen'south modes of limited transposition.
Harmonic content [edit]
The notes of a scale course intervals with each of the other notes of the chord in combination. A 5-note scale has x of these harmonic intervals, a 6-notation scale has 15, a vii-annotation scale has 21, an 8-note calibration has 28.[6] Though the scale is not a chord, and might never be heard more than one note at a time, still the absence, presence, and placement of sure key intervals plays a large part in the sound of the scale, the natural movement of melody within the scale, and the selection of chords taken naturally from the scale.[6]
A musical scale that contains tritones is called tritonic (though the expression is also used for whatsoever scale with but three notes per octave, whether or not it includes a tritone), and one without tritones is atritonic. A scale or chord that contains semitones is called hemitonic, and without semitones is anhemitonic.
Scales in composition [edit]
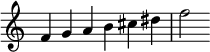
Scales can be bathetic from functioning or composition. They are also ofttimes used precompositionally to guide or limit a composition. Explicit education in scales has been office of compositional training for many centuries. 1 or more scales may exist used in a composition, such as in Claude Debussy'southward 50'Isle Joyeuse.[vii] To the right, the starting time scale is a whole-tone calibration, while the second and 3rd scales are diatonic scales. All three are used in the opening pages of Debussy'south piece.
Western music [edit]
Scales in traditional Western music generally consist of seven notes and repeat at the octave. Notes in the commonly used scales (encounter but beneath) are separated past whole and half step intervals of tones and semitones. The harmonic small scale includes a iii-semitone step; the anhemitonic pentatonic includes two of those and no semitones.
Western music in the Medieval and Renaissance periods (1100–1600) tends to use the white-note diatonic scale C–D–East–F–G–A–B. Accidentals are rare, and somewhat unsystematically used, frequently to avoid the tritone.
Music of the mutual practice periods (1600–1900) uses three types of scale:
- The diatonic calibration (seven notes)—this includes the major scale and the natural modest
- The melodic and harmonic modest scales (vii notes)
These scales are used in all of their transpositions. The music of this period introduces modulation, which involves systematic changes from one scale to some other. Modulation occurs in relatively conventionalized ways. For example, major-mode pieces typically begin in a "tonic" diatonic calibration and modulate to the "ascendant" calibration a fifth above.
In the 19th century (to a certain extent), but more in the 20th century, additional types of scales were explored:
- The chromatic scale (twelve notes)
- The whole-tone scale (half dozen notes)
- The pentatonic scale (5 notes)
- The octatonic or diminished scales (8 notes)

A large variety of other scales exists, some of the more common being:
- The Phrygian ascendant scale (a style of the harmonic minor scale)
- The Arabic scales
- The Hungarian minor scale
- The Byzantine music scales (called echoi)
- The Persian calibration
Scales such every bit the pentatonic scale may be considered gapped relative to the diatonic calibration. An auxiliary scale is a scale other than the main or original scale. See: modulation (music) and Auxiliary diminished calibration.
Notation names [edit]
In many musical circumstances, a specific note of the scale is chosen as the tonic—the fundamental and almost stable note of the scale. In Western tonal music, unproblematic songs or pieces typically start and end on the tonic note. Relative to a choice of a certain tonic, the notes of a calibration are often labeled with numbers recording how many calibration steps above the tonic they are. For case, the notes of the C major scale (C, D, E, F, G, A, B) can be labeled {i, two, three, iv, 5, 6, 7}, reflecting the choice of C as tonic. The expression calibration caste refers to these numerical labels. Such labeling requires the option of a "first" note; hence calibration-degree labels are non intrinsic to the scale itself, merely rather to its modes. For example, if we choose A equally tonic, and then we can label the notes of the C major scale using A = 1, B = 2, C = 3, and so on. When nosotros practice so, we create a new scale called the A minor calibration. See the musical note commodity for how the notes are customarily named in different countries.
The scale degrees of a heptatonic (vii-notation) scale tin likewise exist named using the terms tonic, supertonic, mediant, subdominant, dominant, submediant, subtonic. If the subtonic is a semitone away from the tonic, then it is usually chosen the leading-tone (or leading-note); otherwise the leading-tone refers to the raised subtonic. Also unremarkably used is the (movable do) solfège naming convention in which each calibration caste is denoted past a syllable. In the major scale, the solfège syllables are: do, re, mi, fa, so (or sol), la, ti (or si), do (or ut).
In naming the notes of a scale, it is customary that each scale degree be assigned its own letter of the alphabet proper noun: for instance, the A major calibration is written A–B–C ♯ –D–E–F ♯ –Thou ♯ rather than A–B–D ♭ –D–Eastward–E ![]() –G ♯ . However, information technology is impossible to do this in scales that contain more than seven notes, at least in the English language-language nomenclature system.[8]
–G ♯ . However, information technology is impossible to do this in scales that contain more than seven notes, at least in the English language-language nomenclature system.[8]
Scales may likewise be identified by using a binary system of twelve zeros or ones to represent each of the twelve notes of a chromatic calibration. It is assumed that the scale is tuned using 12-tone equal temperament (so that, for instance, C ♯ is the same as D ♭ ), and that the tonic is in the leftmost position. For example, the binary number 101011010101, equivalent to the decimal number 2773, would represent whatever major calibration (such as C–D–E–F–G–A–B). This organisation includes scales from 100000000000 (2048) to 111111111111 (4095), providing a total of 2048 possible species, merely only 351 unique scales containing from 1 to 12 notes.[ix]
Scales may too exist shown every bit semitones from the tonic. For instance, 0 2 iv v 7 nine 11 denotes any major scale such equally C–D–Eastward–F–1000–A–B, in which the outset degree is, obviously, 0 semitones from the tonic (and therefore coincides with information technology), the second is 2 semitones from the tonic, the third is 4 semitones from the tonic, and so on. Again, this implies that the notes are drawn from a chromatic scale tuned with 12-tone equal temperament. For some fretted string instruments, such as the guitar and the bass guitar, scales can be notated in tabulature, an approach which indicates the fret number and string upon which each calibration caste is played.
Transposition and modulation [edit]
Composers transform musical patterns past moving every note in the pattern by a abiding number of scale steps: thus, in the C major calibration, the pattern C–D–East might exist shifted upwardly, or transposed, a unmarried scale step to go D–E–F. This process is called "scalar transposition" or "shifting to a new primal" and can often be establish in musical sequences and patterns. (It is D-E-F ♯ in Chromatic transposition). Since the steps of a scale can have various sizes, this process introduces subtle melodic and harmonic variation into the music. In Western tonal music, the simplest and most common type of modulation (or changing keys) is to shift from one major fundamental to another cardinal congenital on the first primal's 5th (or dominant) scale caste. In the cardinal of C major, this would involve moving to the key of 1000 major (which uses an F ♯ ). Composers as well often attune to other related keys. In some Romantic music era pieces and contemporary music, composers attune to "remote keys" that are not related to or close to the tonic. An instance of a remote modulation would be taking a song that begins in C major and modulating (changing keys) to F ♯ major.
Jazz and blues [edit]

Through the introduction of blue notes, jazz and blues employ scale intervals smaller than a semitone. The blueish note is an interval that is technically neither major nor small but "in the eye", giving it a characteristic flavour. A regular pianoforte cannot play blueish notes, simply with electric guitar, saxophone, trombone and trumpet, performers tin "bend" notes a fraction of a tone sharp or flat to create bluish notes. For instance, in the key of E, the blue annotation would be either a note between 1000 and 1000 ♯ or a note moving betwixt both.
In blues, a pentatonic scale is often used. In jazz, many unlike modes and scales are used, frequently within the same piece of music. Chromatic scales are common, especially in modern jazz.
Not-Western scales [edit]
Equal temperament [edit]
In Western music, scale notes are often separated by equally tempered tones or semitones, creating 12 intervals per octave. Each interval separates two tones; the higher tone has an oscillation frequency of a fixed ratio (by a factor equal to the twelfth root of two, or approximately 1.059463) higher than the frequency of the lower one. A calibration uses a subset consisting typically of 7 of these 12 as scale steps.
Other [edit]
Many other musical traditions use scales that include other intervals. These scales originate within the derivation of the harmonic series. Musical intervals are complementary values of the harmonic overtones series.[10] Many musical scales in the world are based on this system, except most of the musical scales from Indonesia and the Indochina Peninsulae, which are based on inharmonic resonance of the dominant metalophone and xylophone instruments.
Intra-calibration intervals [edit]
Some scales apply a unlike number of pitches. A common scale in Eastern music is the pentatonic scale, which consists of five notes that span an octave. For example, in the Chinese culture, the pentatonic scale is usually used for folk music and consists of C, D, Eastward, G and A, unremarkably known as gong, shang, jue, chi and yu.[eleven] [12]
Some scales bridge function of an octave; Several such brusk scales are typically combined to course a scale spanning a full octave or more, and usually called with a third name of its own. The Turkish and Middle Eastern music has around a dozen such basic short scales that are combined to form hundreds of full-octave spanning scales. Amid these scales Hejaz scale has i calibration pace spanning 14 intervals (of the centre eastern blazon constitute 53 in an octave) roughly similar to 3 semitones (of the western blazon found 12 in an octave), while Saba scale, another of these heart eastern scales, has iii consecutive scale steps within fourteen commas, i.due east. separated past roughly 1 western semitone either side of the middle tone.
Gamelan music uses a small variety of scales including Pélog and Sléndro, none including equally tempered nor harmonic intervals. Indian classical music uses a moveable seven-note calibration. Indian Rāgas ofttimes use intervals smaller than a semitone.[13] Turkish music Turkish makams and Standard arabic music maqamat may use quarter tone intervals.[14] [ page needed ] In both rāgas and maqamat, the distance between a note and an inflection (east.g., śruti) of that same note may be less than a semitone.
Run into besides [edit]
- List of musical scales and modes
- Melodic blueprint
- Pitch circularity
- Shepard tone
References [edit]
- ^ Benward, Bruce and Saker, Marilyn Nadine (2003). Music: In Theory and Practice, seventh edition: vol. 1, p. 25. Boston: McGraw-Hill. ISBN 978-0-07-294262-0.
- ^ Hewitt, Michael (2013). Musical Scales of the World, pp. 2–3. The Note Tree. ISBN 978-0-9575470-0-one.
- ^ "All The Scales". www.allthescales.org. Archived from the original on fifteen October 2017. Retrieved 28 April 2018.
- ^ Nzewi, Meki, and Odyke Nzewi (2007), A Contemporary Study of Musical Arts. Pretoria: Eye for Indigenous Instrumental African Music and Dance. Volume 1 p. 34 ISBN 978-1-920051-62-four.
- ^ Nettl, Bruno, and Helen Myers (1976). Folk Music in the United States, p.39. ISBN 978-0-8143-1557-6.
- ^ a b Hanson, Howard. (1960) Harmonic Materials of Modernistic Music, pp.7ff. New York: Appleton-Century-Crofts. LOC 58-8138.
- ^ Tymoczko, Dmitri (2004). "Calibration Networks and Debussy" (PDF). Journal of Music Theory. 48 (2): 219–294 (254–264). doi:ten.1215/00222909-48-two-219. ISSN 0022-2909. Archived (PDF) from the original on 9 August 2017. Retrieved 18 July 2017. .
- ^ "C Major Scale". All About Music Theory.com . Retrieved 12 September 2022.
- ^ Duncan, Andrew (1991). "Combinatorial Music Theory". Journal of the Audio Technology Society. 39 (6): 427–448. ISSN 0004-7554. Archived from the original on 7 January 2008. Retrieved 18 July 2017.
- ^ Explanation of the origin of musical scales clarified past a string division method Archived 24 August 2012 at the Wayback Machine by Yuri Landman on furious.com
- ^ Wu, Dan; Li, Chao-Yi; Yao, De-Zhong (i October 2013). "An ensemble with the chinese pentatonic scale using electroencephalogram from both hemispheres". Neuroscience Bulletin. 29 (five): 581–587. doi:10.1007/s12264-013-1334-y. ISSN 1995-8218. PMC5561954. PMID 23604597.
- ^ Van Khê, Trân (1985). "Chinese Music and Musical Traditions of East asia". The World of Music. 27 (1): 78–xc. ISSN 0043-8774. JSTOR 43562680.
- ^ Burns, Edwaard M. 1998. "Intervals, Scales, and Tuning.", p. 247. In The Psychology of Music, second edition, edited by Diana Deutsch, 215–264. New York: Academic Printing. ISBN 0-12-213564-4.
- ^ Zonis [Mahler], Ella. 1973. Classical Persian Music: An Introduction. Cambridge, Massachusetts: Harvard Academy Press.
Farther reading [edit]
- Barbieri, Patrizio (2008). Enharmonic Instruments and Music, 1470–1900. Latina, Italian republic: Il Levante Libreria Editrice. ISBN978-88-95203-14-0.
- Yamaguchi, Masaya (2006). The Complete Thesaurus of Musical Scales (revised ed.). New York: Masaya Music Services. ISBN978-0-9676353-0-nine.
External links [edit]
- Octave Frequency Sweep, Consonance & Noise
- WolframTones—hear and play musical scales
- Visual representation of scales from WolframTones
- ScaleCoding
- Database in .xls and FileMaker formats of all 2048 possible unique scales in 12 tone equal temperament + meantone alternatives.
Part Of A Musical Scale,
Source: https://en.wikipedia.org/wiki/Scale_(music)
Posted by: galindowhistamed1951.blogspot.com


0 Response to "Part Of A Musical Scale"
Post a Comment